Khoa Học Phương Tây và Triết Học Phương Đông (4) -

Kiều Tiến Dũng

Hư không, hữu hạn và vô hạn

Trong cái gọi là “hư không” trong ngoặc kép đã sẵn hàm chứa cái vô hạn. Đây không phải chỉ là ghi nhận của Kinh Dịch, của Đạo Đức Kinh, hay chỉ là lời thuyết giảng của Thích Ca, mà đấy còn là sự thật trong toán học, trong vật lý hiện đại về cái thế giới ngoài kia.

Ánh sáng được cho là một loại sóng điện từ, cũng như sóng radio phát ra từ đài Hồn Việt, hay tia tử ngoại và hồng ngoại phát ra từ mặt trời. Sự khác biệt giữa các loại sóng điện từ này chỉ ở chổ chúng giao động với những tần số khác nhau mà thôi.

Từ cái bản chất là sóng, và cũng như những đợt sóng lăn tăn trên mặt hồ phẳng lặng bị khuấy động bởi những viên sỏi vô tình, ánh sáng cũng cho ta sự nhiễu xạ và giao thoa. Nhất là sự giao thoa khi những đợt sóng gặp nhau thì có chổ chúng bồi đắp cho nhau, đồng thời cũng có nơi chúng triệt tiêu lẫn nhau.

Qua sự giao thoa ánh sáng này ta có thể dựng được những hình nổi ba chiều trong kỹ thuật holograms. Để ghi nhận hologram của một vật thể ba chiều ta dùng một luồng ánh sáng laser tách làm hai tia: một tia chiếu thẳng vào tấm phim chụp, tia kia chiếu vào vật thể ba chiều để gần tấm phim chụp đó. Vì vậy, thay vì ghi lại trên phim chụp là cái bóng của vật thể như những hình chụp thông thường, nay trên đó ta lại có sự giao thoa giữa các tia sáng phản chiếu từ vật thể với tia sáng laser thứ nhất. Nhìn kỷ thì tấm phim không có hình bóng gì của vật thể cả, mà chỉ có những sợi vân đen trắng, như vân tay của ta, hình thành từ sự giao thoa ánh sáng.

Sau đó, khi ta đem chiếu tia laser vào tấm phim hologram đó thì các tia phản chiếu từ đó sẽ tạo ra một hình thể ba chiều của vật thể ta đã chụp lúc ban đầu. Ngày nay holograms được dùng nhiều trên các thẻ tín dụng (credit cards) như một dụng cụ chống giả mạo.

Hologram là một khám phá kỳ thú trong quang học, là hệ quả của sự giao thoa ánh sáng. Đây cũng là điều mà chúng ta sẽ bàn nhiều trong các bài sau. Điều tôi muốn trình bày ở đây là khi ta cắt đôi cái hologram thì nửa cái hologram vẫn có thể cho ta lại hình ảnh khái quát của vật thể, có mất đi chỉ là các chi tiết li ti của vật thể đó mà thôi. Và cứ thế, ta càng cắt vụn tấm hologram thì các chi tiết tuy bị mất đi, nhưng cái bao quát vẫn còn đó!

Đây là điều khác biệt với một tấm ảnh bình thường: khi tấm ảnh bình thường bị xé nhỏ ra thì ta mất đi cái hình thể bao quát, chỉ còn lại các chi tiết nhỏ nhoi. Trái lại, phần nhỏ nhất của hologram lại chứa đựng những dữ kiện về hình dạng bao quát nhất của vật thể; và cần phải có toàn bộ tấm hologram thì ta mới có thể tái lập được các chi tiết li ti của vật thể.

Hologram là một ví dụ cụ thể trong vật lý về cái ẩn tàng của cái lớn nhất trong cái bị coi là nhỏ nhất. Nhỏ nhất về mặt kích thước nhưng lại to lớn về mặt nội dung!

Nhưng có lẽ ta cũng không cần khoa học để có thể hiểu được rằng cái nhỏ bé lại có thể chứa đựng cái to lớn. Thi sĩ Thâm Tâm trong bài Tống Biệt Hành cũng đã biết rằng:

“Đưa người ta không đưa sang sông,
Sao có tiếng sóng ở trong lòng?
Bóng chiều không thắm, không vàng vọt,
Sao đầy hoàng hôn trong mắt trong?”

“Sao đầy hoàng hôn trong mắt trong!” Ôi, đôi mắt nhỏ bé lại có thể chứa đựng cả đất trời, lại có thể dậy sóng nhận chìm cả hồn người. Nếu chẳng phải thế thì Khái Hưng đâu đã phải than rằng: “Chí lớn trong thiên hạ không đựng đầy đôi mắt mỹ nhân.”

Trang Tử trong Nam Hoa Kinh cũng cho rằng “Thiên tại nội, nhân tại ngoại.” Ở bề ngoài tuy con người là hữu hạn với thất tình lục dục, tử sinh vô định, thì ngay bên trong đã chứa sẵn cái Đạo thể vô cùng. Còn theo như nhà phật thì ngay trong cái tôi luôn biến chuyển của mỗi cá nhân, tức là ngay trong cái tiểu ngã vô thường của mỗi con người, luôn có sẵn cái phật tánh, cái đại ngã vĩnh hằng bất biến.

Kinh Dịch cũng thế: “Thái Cực dã, đại tắc bao thiên địa, tiểu tắc nhập giới tử” — cái gọi là Thái Cực lớn thì trùm trời đất, mà nhỏ thì lọt trong cái nhỏ nhất. Thái Cực vừa là cực đại, vừa là cực tiểu. Cực đại nên bao trùm vũ trụ muôn phương, cực tiểu nên lồng trong giới tử. Dù nhìn bao quát cả vũ trụ cũng chỉ có một Thái Cực, nhưng nếu nhìn tán phân từng vật, ta lại thấy mỗi vật đều gồm đủ cả Thái Cực. Thái Cực tuy sản sinh Vạn Hữu, nhưng không vì thế mà bị hao mòn, sau trước vẫn là duy nhất và bất khả phân.

Cái hữu hạn lại có thể chứa đựng cái vô hạn. Đây không phải là điều vô lý vì cái ta thấy được chỉ là một phần hữu hạn của cái bản thể vô hạn.

Nếu thêm vào cái chiều thời gian thì ta chẳng ngạc nhiên khi cái thai nhi nhỏ bé trước đó đã chứa đựng mọi cấu trúc hình thể của chú voi to lớn sau này. Cũng vậy, một hành vi tuy nhỏ nhặt nhưng nhiều khi lại là cái nhân cho những biến cố trọng đại trong tương lai.

Người ta đã từ lâu có khái niệm về cái vô cùng to, và cái vô cùng nhỏ. Nhưng chúng cũng đã gây không biết bao tranh cãi cho các nhà triết học và toán học. Thế nào là to lớn vô cùng? Vũ trụ có phải vô cùng hay không? Có gì ở ngoài vũ trụ này không, và do đó phải to hơn cái vô cùng? Cái nhỏ nhất, mặt khác, có thể chia được nữa không?

Một phần của những câu hỏi này đã được đúc kết trong cái gọi là nghịch lý của Zeno, một triết gia Hy Lạp cổ. Zeno cho rằng một chú thỏ khởi hành sau một cụ rùa sẽ không bao giờ bắt kịp cụ rùa! Ông lý luận như sau: muốn bắt được rùa thì thỏ trước hết phải rút ngắn được một nửa cái khoảng cách giữa mình và rùa lúc ấy; sau đó thỏ lại phải rút ngắn được một nửa cái khoảng cách còn lại giữa mình và rùa. Và cứ thế, thỏ phải mãi tiếp tục rút ngắn một nửa cái khoảng cách còn lại –hoài hoài không bao giờ xong. Và do đó không bao giờ bắt kịp được rùa! Rõ ràng đây là điều không ổn.

Cái nghịch lý này chỉ được giải thích thỏa đáng hơn 2000 năm sau đó qua toán học vi phân và tích phân của Leibniz-Newton.

Khoảng 200 năm sau Zeno thì ở phương đông cũng có Trang Tử với cái suy nghĩ y hệt như vậy: “Nhất xích chi chủy, nhật thủ kỳ bán, vạn thế bất kiệt” — gậy dài một thước, mỗi ngày chặt một nửa, chặt hoài suốt bao đời cũng không hết. Trong cái hữu hạn của một thước gậy dường như đã chứa đựng cái vô hạn.

Nhưng điều vô cùng ngạc nhiên là, trong một thời gian rất dài, toán học đã không tiến tới từ cái rất nhỏ đến con số không. Con số không quen thuộc với ta, tưởng chừng không thể thiếu được trong cuộc sống hàng ngày thật ra chỉ bắt đầu xuất hiện vào thế kỷ thứ tư sau công nguyên trong nền văn minh Mayan ở Nam Mỹ. Nền văn minh này sau đó bị hủy diệt hoàn toàn một cách bí ẩn. Rồi vào thế kỷ 6, con số không mới lại được đưa vào toán học ở Ấn Độ. Tây phương phải đợi đến thế kỷ 12 thì con số không mới được du nhập, vay mượn từ Ấn Độ!

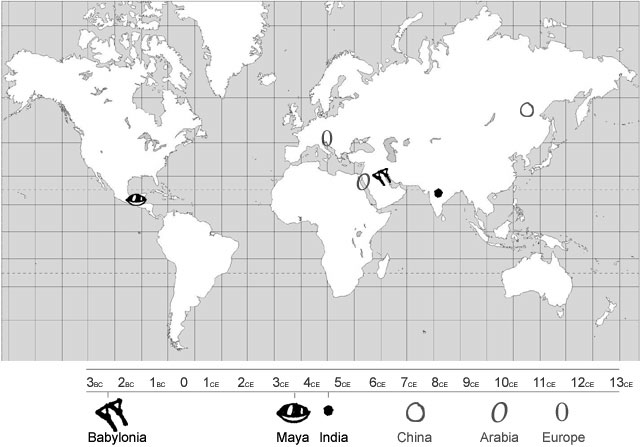
Lịch sử của zero. Nguồn: mediatinker.com

Phải chăng nhờ có cái khái niệm “hư không” từ Ấn Độ Giáo và Phật Giáo trước đó nên con số không mới dễ mọc rễ và hình thành ở Ấn Độ?

“Không” ở đây có nghĩa là không có. Nhưng đó lại là cái nghịch lý trong lối suy nghĩ toán học ở phương tây. Khái niệm “một, hai” thì dễ hiểu: hai trái táo dĩ nhiên khác hai trái lê; nhưng đã là không thì không táo cũng như không lê, thậm chí cũng chẳng khác gì không chó, không mèo! Đã là không rồi thì có gì nữa đâu mà nói, có cần gì nữa đâu mà phải ký hiệu nó bằng một con số trong toán học!

Và rồi khi toán học có được nó thì nó lại tạo ra cái nhức đầu khác. Cộng, trừ, nhân với số không thì cũng được đi. Nhưng thế nào là chia cho số không? Một gia tài chia đôi thì hai người được hưởng, mỗi người một nửa; gia tài chia một thì một mình ta hưởng. Càng chia cho con số càng nhỏ, cho ít người thì ta càng được phần lớn.

Còn đem gia tài chia cho số không nghĩa là gì?

Nếu cứ theo cái đà “càng chia cho con số càng nhỏ, cho ít người thì ta càng được phần lớn” thì ta sẽ phải đi đến kết luận là chia cho zero là một con số thật lớn, là con số vô cực, vô cùng – infinity. Nhưng đấy lại là điều không ổn!

Lấy 6 chia cho 2 thì được 3, nói cách khác 6 bằng 2 nhân cho 3. Cũng vậy, nếu lấy 1 chia cho zero để được vô cực, thì 1 sẽ bằng zero nhân cho vô cực. Rồi lấy 2 chia cho zero để được vô cực, thì 2 cũng sẽ bằng zero nhân cho vô cực. Và rồi cũng như A=B và C=B thì A phải bằng C, nếu 1 và 2 đều bằng zero nhân cho vô cực thì chúng sẽ phải bằng nhau.

Chúng ta vừa “chứng minh” xong là 1 phải bằng 2! Từ đó tất cả các con số khác sẽ đều bằng nhau! Tóm lại, theo như trên đây từ con số không, ta đã phải có con số vô cực. Rồi từ đó ta lại phải đi đến kết luận tất cả các con số đều như nhau, kể cả số không và số vô cực cũng như nhau!

Với những lập luận và kết quả trên, dường như từ toán học ta đã “chứng minh” được Dịch, được Lão Tử, Thích Ca: “từ không đến vô cực, từ vô cực trở về không, và bản thể của muôn loài là như nhau.”

Đây dĩ nhiên là vô lý, và các lý luận toán học trên đây là ngụy biện vì chúng chứa đựng các mâu thuẩn nội tại.

Toán học không thể có những mâu thuẩn nội tại như vậy. Toán học đã cố gắng tránh khỏi cái khó khăn này bằng cách khẳng định vô cực là một khái niệm, nó không phải là một con số như những con số khác. Kết quả của việc chia cho số không, zero là một khái niệm chứ không phải là một con số.

Giải quyết đấy cũng chỉ là tạm thời thôi, cho đến thế kỷ 19 khi Goerg Cantor đặt lại vấn đề về khái niệm vô cực.

**
Georg Cantor là một nhà toán học người Đức sống vào cuối thế kỷ 19. Ông đã dám mở cửa cánh thiên đường của vô cực (infinity) và phân loại chúng.

Các con số nguyên 1, 2, 3, 4 … dần dần dẫn ta đến vô cực. Đây là loại vô cực được kịch tính hóa qua cái gọi là “Khách Sạn Hilbert,” một khách sạn tuy có vô số phòng nhưng nay đã hết phòng, no vacancy. Không hề gì, khi có khách mới thì người quản lý chỉ cần yêu cầu vị khách đang ở phòng số 1 dời qua phòng 2, khách phòng 2 dời qua phòng 3, và cứ thế tiếp tục. Kết quả là phòng số 1 nay đã trống để cho vị khách mới này.

Thiên đàng luôn còn chổ trống cho những ai tìm đến. Chỉ tiếc rằng trái tim con người không được như thế mà lại quá hạn hẹp, nhỏ nhoi, ngay cả với đồng loại của mình!

Nhưng Cantor đã nhận ra rằng loại vô cực trên đây lại khác hẳn và “nhỏ hơn” tổng số các con số thực. Số thực bao gồm các số nguyên 1, 2, 3 … và luôn cả các số “vô tỷ” (irrational numbers như căn bậc hai của 2 không thể diễn tả bằng một phân số. Số thực cũng bao gồm những số gọi là “siêu việt” (transcendental numbers) như số Pi (3.14159 …). Vì số thực bao gồm số nguyên nên phải “nhiều” hơn số nguyên. Do đó chỉ có thể kết luận là tổng số các con số thực phải là một khái niệm vô cực lớn hơn cái vô cực của các con số nguyên. Vô cực của các con số nguyên là vô cực đếm được (countable infinity); vô cực của các số thực là loại vô cực không đếm được (uncountable infinity).

Và cứ thế, qua cái tư duy vô hạn trong một thân thể hữu hạn, Cantor đã tìm ra vô số các vô cực khác, và xếp loại chúng, cái sau bao gồm cái trước. Trên vô cực lại có vô cực, và cứ thế lại có vô số các vô cực.

Cao nhân tắc hữu cao nhân trị; ngoài trời còn có trời!

Nhưng lại khốn khổ thay cho Cantor vì ông đã dám bàn về vô cực, những cái “thiêng liêng” không được quyền nói đến.

Con đường dẫn tới chân lý đầy rẫy những hy sinh, gian khổ. Những kẻ đi trước nhân loại đều bị coi là bất thường, nhiều khi là điên khùng, bị xa lánh, và đôi khi bị chống đối, phỉ báng.

Thiên tài và người điên có khác nhau bao nhiêu đâu khi họ đều là những người sống ngoài những ràng buộc, định kiến của xã hội; có những suy nghĩ bất chấp những khuôn đóng tư tưởng sẵn có. Và thường thì họ đã phải trả những cái giá đắc. “Chữ tài liền với chữ tai một vần.”

Galilei Galileo thì bị Giáo Hội La Mã trù dập, kết án và sau cùng bị tước hết mọi quyền nghiên cứu khoa học. Georg Cantor thì đã bị đồng nghiệp, và ngay cả thầy dạy của mình đả kích kịch liệt, dằn vặt cho đến phải vào bệnh viện tâm thần, rồi chết ở đấy trong cơn điên loạn.

Ludwig Boltzmann, một nhà vật lý cùng thời, cũng có một số phận không tốt đẹp gì hơn. Boltzmann là người đề ra căn bản vi mô cho khái niệm Entropy. Nhưng lúc ấy, vào thế kỷ 19, người ta không tin vào cấu trúc nguyên phân tử của vật chất nên đã hè nhau chống đối và nhạo báng ông. Không có ai hiểu được mình, không có ai là tri kỷ, Boltzmann đã không thể:

“Vỗ gươm mà hát, nghiêng bầu mà hỏi
Trời đất mang mang
Ai người tri kỷ…
Lại đây cùng ta
Chung cạn một hồ trường!”

(Nguyễn Bá Trác dịch từ “Nam phương ca khúc”, chương 10 tập “Hạn mạn du ký”)

Trích đoạn từ Nam phương ca khúc (南方歌曲) .Nguồn: Nam Phong tạp chí số 41 năm 1920, trang 400–401.

Sau cùng, Boltzmann lại đi chọn lối thoát qua sự tự sát. Ngày nay trên mộ bia của Boltzmann ở Vienna, thủ đô của nước Áo, còn khắc lại cái công thức để đời của ông như một món quà cho nhân loại, và cũng như một tuyên ngôn chiến thắng đối với những kẻ đã một thời nhạo báng mình.

Định luật trong khoa học, triết học có thể là khách quan, nhưng con đường dẫn đến chúng lại mang đầy tính chất nhân bản, với biết bao bi hài kịch trên sân khấu cuộc đời.

Phải chăng vô cực chỉ là một khái niệm thuần túy chỉ có trong toán học không? Theo Thuyết Trường Lượng Tử (Quantum Field Theory) của thế kỷ 20, thì “Không.” Cái thực thể ngoài kia đã hàm chứa sẵn cái vô hạn.

Thuyết Lượng Tử Điện Từ Trường (Quantum Electrodynamics) là sự kết hợp của Thuyết Tương Đối Hẹp và Cơ Học Lượng Tử. Riêng lẻ thì Thuyết Tương Đối Hẹp và Cơ Học Lượng Tử đã là thành công vượt bực, nhưng khi gộp chung chúng lại thì Thuyết Lượng Tử Điện Từ Trường được coi là thành công nhất trong lịch sử khoa học từ trước tới nay: các tiên đoán của thuyết này được xác nhận với độ chính xác chưa từng có với cái sai số chỉ ở một phần trong một tỷ phần!

Từ cái vô hạn, sinh ra cái hữu hạn; rồi từ cái hữu hạn lại trở về cái vô hạn. Thật ra cái hữu hạn đã “chứa” sẵn cái vô hạn! Hơn thế nữa, bản thể của mọi hiện tượng đều đến từ cái được gọi là “hư không”!

Những khẳng định trên đây tưởng như là từ triết học mà thật ra cũng lại là từ khoa học, từ Thuyết Lượng Tử Điện Từ Trường mà chúng ta sẽ bàn tới trong bài kế. Ở đây tôi xin kết thúc với một bài học khác rút tỉa từ cái không và cái vô hạn.

Nếu mặt trăng là cứu cánh thì ta phải quên đi ngón tay chỉ trăng mà hướng về mặt trăng. Ngón tay chỉ trăng chỉ là phương tiện để hướng về cứu cánh là mặt trăng. Chiêu thức trong võ thuật cũng chỉ là phương tiện. Đỉnh tối cao chỉ có thể đạt được khi Lệnh Hồ Xung đã quên hết chiêu thức, để lấy vô chiêu mà thắng hữu chiêu.

Nếu muốn đạt được giác ngộ thì có lúc ta phải quên đi kinh điển; khi đã qua tới bờ ngộ thì hãy quên đi ghe thuyền. Cũng giống như nhờ nơm mà bắt được cá, được cá thì bỏ nơm. Nhờ lời mà hiểu ý, được ý thì quên lời. Chứ cứ khư khư ôm lấy kinh điển, ôm lấy ghe thuyền khi chúng chỉ là những phương tiện thì làm sao ta đi tới được cái cứu cánh giác ngộ?

Nhưng cứu cánh không phải là tất cả, bất chấp mọi phương tiện. Sử dụng phương tiện thích hợp để rồi quên chúng đi không có nghĩa là phương tiện nào cũng dùng, bất chấp, bất kể.

Lấy ví dụ cái tỷ số a/b khi cả hai a và b đều bằng zero. Nhưng lấy zero chia cho zero lại là vô định, bằng bao nhiêu cũng được do đó nó là vô nghĩa. Còn nếu ta biết được thí dụ như a=2c, b=3c và c tiến về zero thì a và b cũng tiến vè zero. Lúc ấy cái tỷ số a/b sẽ có ý nghĩa và bằng 2c/(3c), đơn giản c đi thì còn lại là 2/3. Cái tỷ số a/b sẽ mang ý nghĩa là 2/3, mặc dù cả a, b lẫn c đều tiến về zero một cách riêng lẻ. Cái ý nghĩa của tỷ số a/b chỉ có được qua chính con đường a và b đã tiến về zero như thế nào mà thôi.

Cũng vậy, Cantor cũng đã phải dựa vào chính các con đường dẫn tới vô cực để định nghĩa và phân loại những cái gọi là vô cực đó. Cứu cánh cũng thế, cũng như vô cực, tự nó không có ý nghĩa. Chính con đường đi đến cái cứu cánh đó mới mang lại cho nó cái ý nghĩa đích thực.

Con đường đi đến cứu cánh, do đó, cũng là quan trọng; đôi khi còn quan trọng và cấp bách hơn chính cái cứu cánh đó. Cứu cánh thì còn quá xa, con đường lại ở ngay trước mắt, ngay trong thời điểm này. Chữ Đạo trong Đạo Đức Kinh vừa có nghĩa là con đường, là phương tiện, vừa có nghĩa là cái sự thật tuyệt đối, là cứu cánh. Không thể tách rời phương tiện ra khỏi cứu cánh.

Nhất là không có thể đem cái cứu cánh thiên đường cộng sản bánh vẽ để ngụy biện cho các phương tiện chuyên chính tàn ác, không tính người, phản dân tộc: đem con đấu tố cha, tù đày người yêu nước, đi buôn dân kiếm tiền, đem nước đi bán để củng cố ghế ngồi.

Không thể tách rời phương tiện ra khỏi cứu cánh; nhưng cũng phải định rõ đâu là cứu cánh, đâu là phương tiện. Chủ nghĩa là cứu cánh hay chính hạnh phúc của con người, dân tộc mới là cứu cánh?

Người dân Việt cần sống, sống cho đúng nghĩa của một con người –ngay bây giờ, ngay ngày hôm nay. Không phải cứ hy sinh mãi cho một thế giới bánh vẽ cứ luôn được định hướng nhưng đi hoài không tới. Nòi giống Việt cần giang sơn cha ông để lại, cần đất sống cho các thế hệ mai sau, chứ cần chi một đảng phái — nhất là một đảng phái vong bản.

Melbourne, Úc Châu
Tháng 7, 2013

Đọc Bài 1; Bài 2; Bài 3;

Nguồn: Bài đã phát thanh do Hồn Việt Radio gởi đến DCVOnline.net.